Publications
publications by categories in reversed chronological order. generated by jekyll-scholar.
-
-
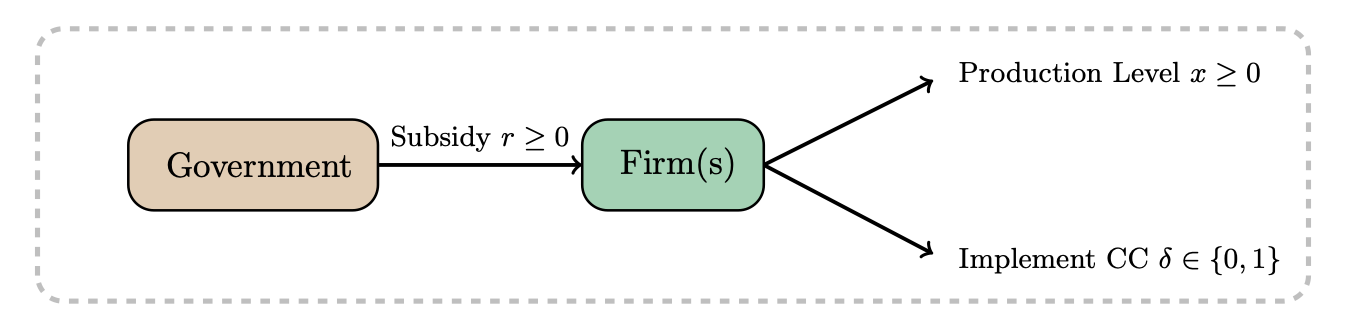 (In review at Energy Policy), 2025
(In review at Energy Policy), 2025- IISE Energy Systems Division Best Student Paper Award, 2025
-
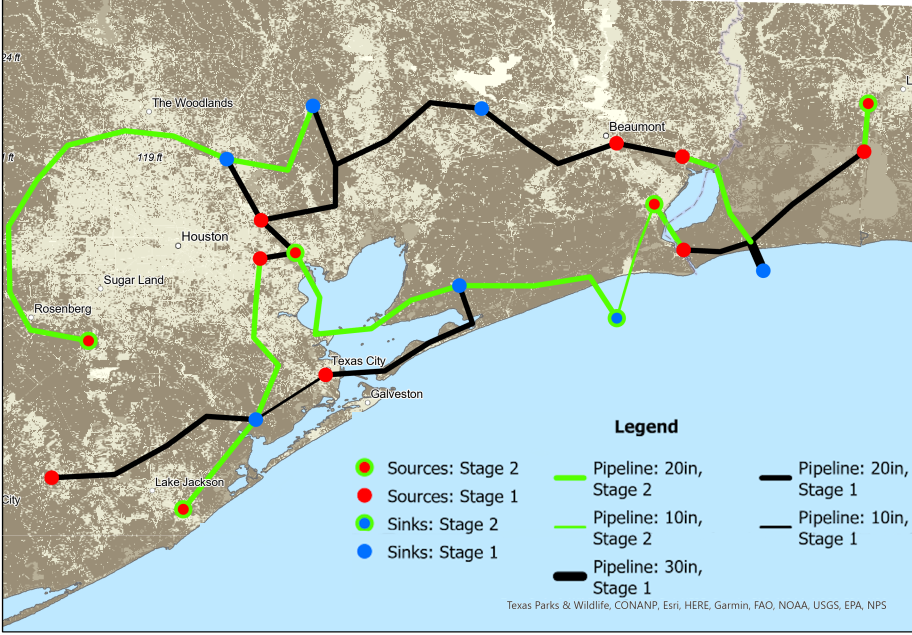 Energy Policy, 2024
Energy Policy, 2024- Dennis J. O’Brien USAEE Best Student Paper Award, 2023
-
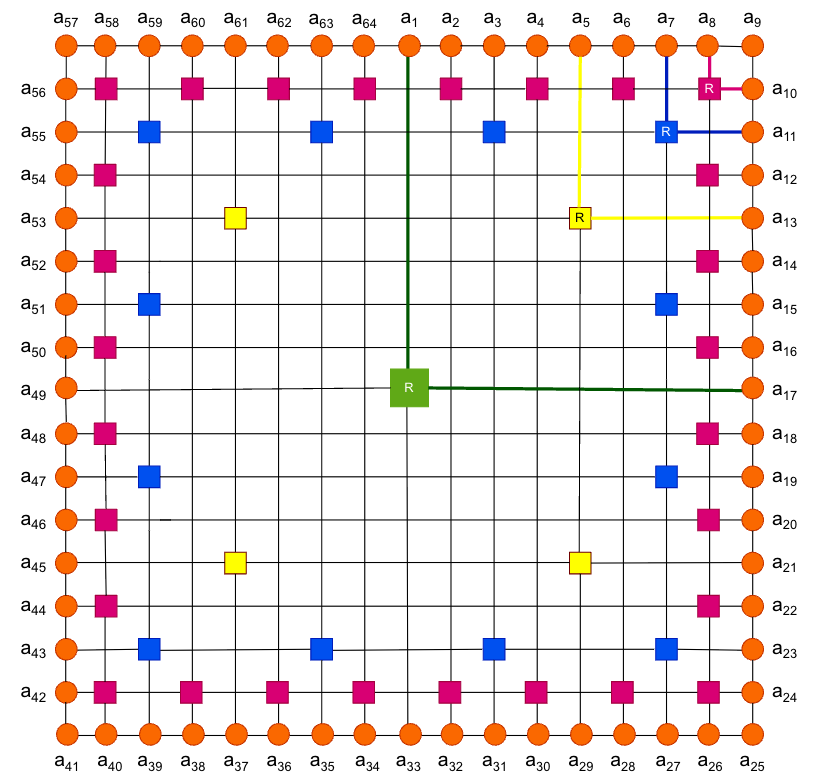 Reliability Engineering & System Safety, 2024
Reliability Engineering & System Safety, 2024 -
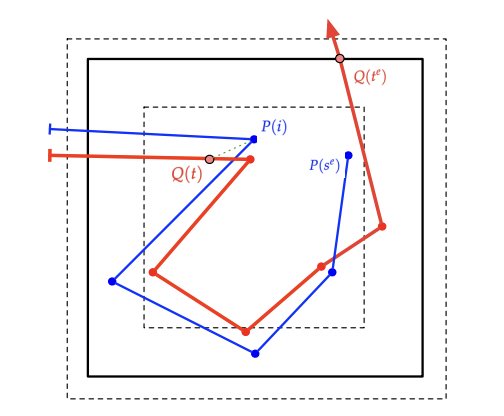 Proceedings of the 37th International Symposium on Computational Geometry (SoCG), 2021
Proceedings of the 37th International Symposium on Computational Geometry (SoCG), 2021
