The Amoeba Problem
First post! Solution to a classic interview problem
Problem Statement
You start off with one amoeba. Every minute, this amoeba can either:
- Do nothing
- Die
- Split into two amoebas
- Split into three amoebas
Each of these actions has an equal probability of occurring. All further amoebas behave the exact same way. What is the probability that the amoebas eventually die off?
Challenge: Suppose now the amoeba has the ability to split into up to \(n\) amoebas. For large \(n\), what is probability that the amoebas eventually die off now?
Solution
Let \(p\) be the probability that an amoeba and all of its decedents eventually die out. We can then calculate this probability by conditioning on each of the actions the amoeba could take
\[\begin{align} p = \frac{1}{4} +\frac{1}{4} p+ \frac{1}{4} p^2 + \frac{1}{4} p^3. \label{eq:n4} \end{align}\]Each term on the right hand side representing the events that the amoeba dies, does nothing, splits in two, and splits in three respectively. Since the any two amoeba’s behave independently of one another, if there are \(k\) amoebas, the probability that all \(k\) and their respective descendants dies out is \(p^k\). Solving for \(p\) in (\ref{eq:n4}), yields two solutions in \([0,1]\). Namely, \(p = 1\) and \(p = \sqrt{2} - 1\). But which of the two is the solution?
We can show that that \(p = \sqrt{2} - 1\) is indeed the correct solution by considering the probability that a given amoeba and its ancestors die out in at most \(k\) minutes, denoted \(P_k\). We can show that for any \(k \geq 1\), \(P_k\) is bounded above by \(\sqrt{2} - 1\) and therefore can never approach \(1\).
We can prove this by induction. Clearly \(P_1 = \frac{1}{4}\) since there is only one way for the a given amoeba to last one minute and \(\frac{1}{4} < \sqrt{2} - 1\). Assume this holds for \(k\). What is the probability a given amoeba and its ancestors die out in at most \(k + 1\) minutes? Well from (\ref{eq:n4}) we have \(\begin{align*} P_{k+1} & = \frac{1}{4} +\frac{1}{4} P_{k}+ \frac{1}{4} P_{k}^2 + \frac{1}{4} P_{k}^3 \\ & = \frac{1}{4}\left( 1 + P_k + P_k^2 + P_k^3\right) && (\text{Plug in } P_k < \sqrt{2} - 1) \\ & < \sqrt{2} - 1 \end{align*}\)
completing our inductive step. Thus as \(k \to \infty\) our probability of extinction \(P_\infty = p\) can never get to 1. Implying the only possible solution is \(\boxed{ p = \sqrt{2} - 1}\).
If we consider the case where now the amoeba now has the options to split into as many as \(n\) amoebas, can we get an estimate of \(p\)? It turns out we can!
Consider the generalized form of (\ref{eq:n4})
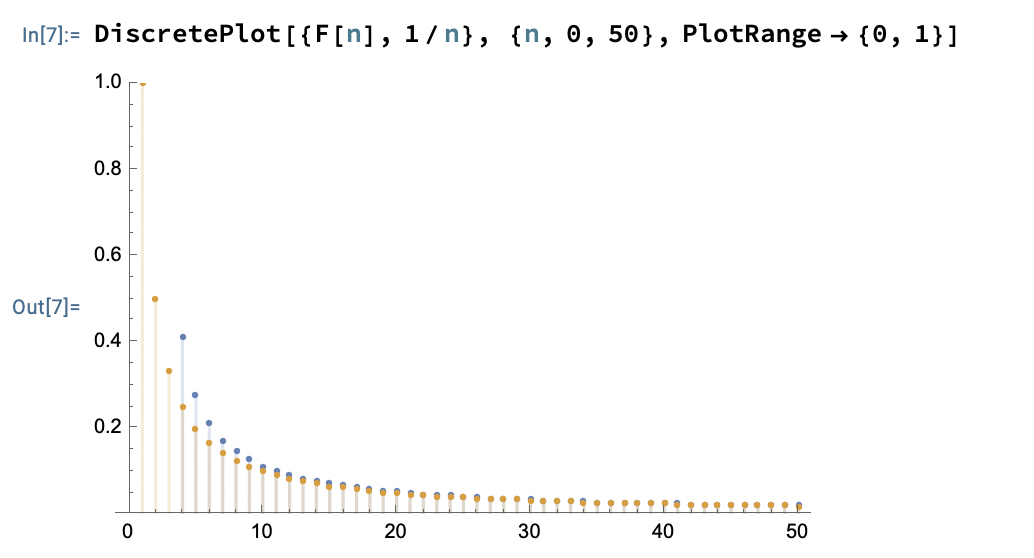
\[\begin{align} p & = \frac{1}{n+1}\sum_{k=0}^n p^k\\ & =\frac{1}{n+1}\left(\frac{1-p^{n+1}}{1 - p}\right)\\ \implies & \\ p (n+1) & = \frac{1-p^{n+1}}{1 - p} \label{eq:gen}. \end{align}\]Note that for large \(n\), the value of \(p = \frac{1}{n+1}\) begins to approximate the solution to (\ref{eq:gen}). We plotted the numerical solution to (\ref{eq:gen}) as function of \(n\) (labeled \(F[n]\) in the figure) and the function \(g(n) = 1/n\) and from the figure below we can see they begin to agree very quickly!