Throwing Darts
Problem Statement
Jason throws two darts at a dartboard, aiming for the center. The second dart lands farther from the center than the first. If Jason throws a third dart aiming for the center, what is the probability that the third throw is farther from the center than the first? Assume Jason’s skillfulness is constant.
Challenge: What if, after the first, his next \(n − 2\) throws are further from the center than the first? What is the probability that the \(n\)-th throw is farther from the center than the first?
Solution
At first glance, it may seem that the information about the second throw is irrelevant. However, we shall see that that is not the case. We will present two solutions to this problem, both interesting in their own right. The first is perhaps a more traditional computational approach to the problem, and the second uses a cheeky symmetry argument.
Solution 1
We will solve the general problem and apply it to the \(n = 3\) case. Let \(R_1,R_2,\ldots, R_n \in [0,1]\) be i.i.d. random variables denoting the radii at which each of the consecutive dart throws land. We would like to evaluate \(\begin{equation} \mathbb{P}\left[R_n > R_1 | R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\right] \end{equation}\)
Using Bayes Theorem, we can write this as \(\begin{equation} \mathbb{P}\left[R_n > R_1 | R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\right] = \frac{\mathbb{P}\left[R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\ \cap \left(R_{n} > R_1\right)\right]}{\mathbb{P}\left[R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\right]} \label{eq:solu}. \end{equation}\)
Now it suffices to evaluate \(\begin{equation} \mathbb{P}\left[ \cap_{i = 2}^n R_{i} > R_1\right] \label{eq:key}. \end{equation}\) In order to do this, we will need to know the probability distribution function for \(R\), denoted \(f(r)\). We can deduce this by considering the unit circle (dartboard) and imagine a thin concentric ring at radius \(r\) of width \(dr\). The area of this ring is \(2 \pi r \; dr\), the area of the circle is \(\pi\) and thus the probability of Jason throwing a dart and it landing at radius \(r\) is \(f(r) = 2 r \; dr\) (see Figure 1).
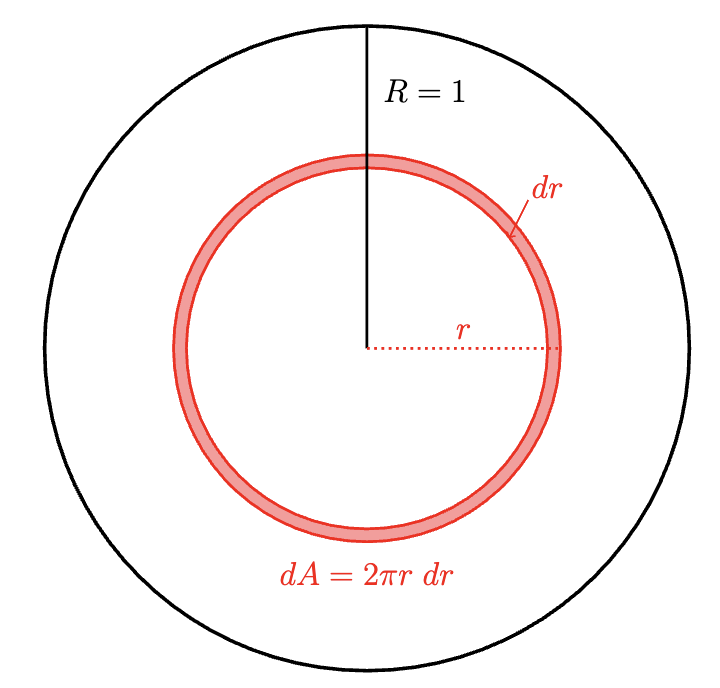
This then implies,
\[\begin{equation} \mathbb{P}\left[R > r\right] = \mathbb{P}\left[R \geq r\right] = 1 - r^2. \end{equation}\]We can then evaluate (\ref{eq:key}) by conditioning on the value of \(R_1\).
\[\begin{align*} \mathbb{P}\left[ \cap_{i = 2}^n R_{i} > R_1\right] & = \int_0^1 (1-r^2)^{n-1} 2 r \; dr \\ & = 2 \int_0^1 (1-r^2)^{n-1} r \; dr \\ & = 1/ n. \end{align*}\]Based on this, we can write (\ref{eq:solu}) as
\[\begin{align*} \mathbb{P}\left[R_n > R_1 | R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\right] & = \frac{\mathbb{P}\left[R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\ \cap \left(R_{n} > R_1\right)\right]}{\mathbb{P}\left[R_2 > R_1 \cap \cdots \cap R_{n-1} > R_1\right]} \\ & = \frac{1/n}{1/(n-1)}\\ & = \frac{n-1}{n}\\ & = \boxed{1 - \frac{1}{n}}. \end{align*}\]Plugging in \(n = 3\) yields the solution to our original problem \(\boxed{2/3}\).
Solution 2
Imagine that all of the throws have already occurred and we are revealing them one at a time. Up until the final throw, the first throw is the closest to the center of the dartboard. We are asked to find, given this knowledge, what is the probability that the first throw is the closest of all of the throws. At this point, the only way this could not be the case if is the last throw is the closest to the center of the \(n\) throws. Since his skill is constant, the probability that his last throw is the closest to the center is the same as for any other throw, \(1/n\). Therefore, the probability that the first throw was the closest of the \(n\) throws given it was closer than the next \(n-2\) throws is \(\boxed{1 - \frac{1}{n}}\).