Jane Street Puzzle August 2024

My solution to last month's puzzle

Tree-Edge Triage

It has become a hobby of mine to work on the monthly Jane Street Puzzle. They usually pose some interesting math or programming problem and I have learned a lot from solving them. Last month’s puzzle was a game played on an infinite binary tree with a surprising result! The problem is as follows:

Aaron and Beren are playing a game on an infinite complete binary tree. At the beginning of the game, every edge of the tree is independently labeled $A$ with probability $p$ and $B$ otherwise. Both players are able to inspect all of these labels. Then, starting with Aaron at the root of the tree, the players alternate turns moving a shared token down the tree (each turn the active player selects from the two descendants of the current node and moves the token along the edge to that node). If the token ever traverses an edge labeled B, Beren wins the game. Otherwise, Aaron wins.

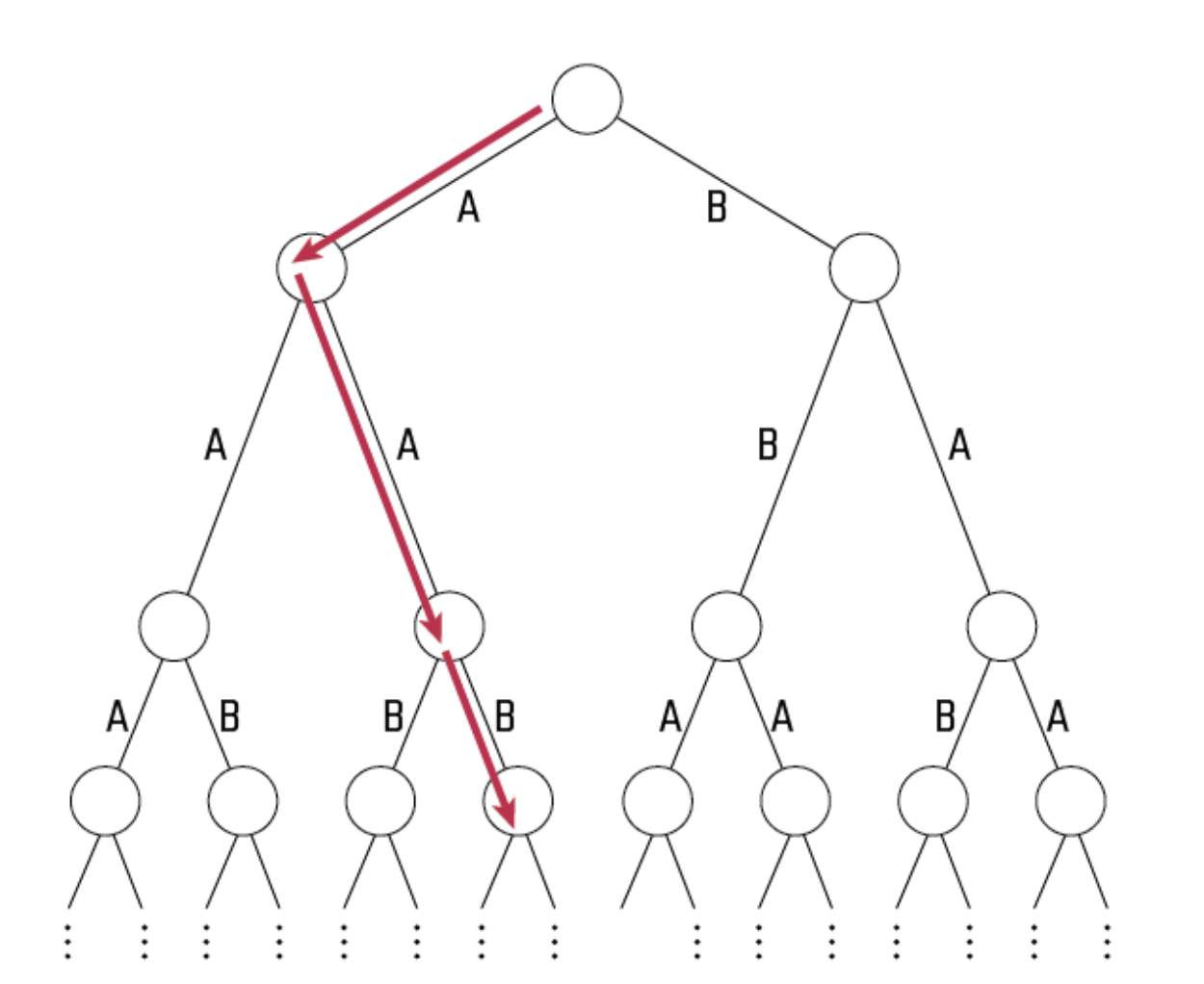
An example game is in the picture above: after the labeling, Aaron chooses to go left to avoid immediate defeat, but after Beren goes right Aaron is doomed to choose one of two B paths and Beren wins.

What is the infimum of the set of all probabilities $p$ for which Aaron has a nonzero probability of winning the game? Give your answer in exact terms.

Solution

The intuition behind my approach was to use the symmetry of an infinite binary tree. Once you move along an edge to a given node, you are once again faced with an infinite binary tree and it’s like you started from the beginning again. By that logic, it is sufficient to analyze the optimal strategy for the first two levels and we can let recursion handle the rest.

Suppose we are considering what Aaron should do on a given turn. On every $A$ (odd) turn, Aaron wins if and only if the current node has at least one $A$ edge out of it that leads to a node with two $A$ edges and each of these edges has a winning $A$ path out of it.

We can write this using a recurrence relation. Let $Q_A$ be the probability that, on an $A$ turn, $A$ can win from the current node from it. Similarly, let $Q_B$ be the probability that at our current node on a $B$ turn, it is one from which $A$ can win.

We have the relation

\[\begin{align} Q_A & = p^2(\underbrace{Q_B^2 + 2Q_B(1-Q_B)}_{\text{Pr at least one winning path out}}) + 2p(1-p)Q_B \\ Q_B & = p^2 Q_A^2. \end{align}\]

The fist equation represents the cases where we are on Aaron’s turn and either:

The second equation represents the case where we are on Beren’s turn and:

Plugging in the latter equation into the former yields the equation for $Q_A$ in terms of $p$

\(\begin{equation}Q_A = 2p^4 Q_A^2 - p^6 Q_A^4 + 2p^3(1-p)Q_A^2 \implies \boxed{Q_A(-p^6 Q_A^3 + 2p^3Q_A - 1) = 0} \end{equation}\) Now if we want to find the values of $p$ for which there is a non-negative value for $Q_A$, the probability of Aaron winning the game from the first move, then we need to find the smallest value of $p$ for which \(p^6 Q_A^3 - 2p^3Q_A + 1 = 0\) has a positive solution when we solve for $Q_A$.

We can plug this into Mathematica and get the closed form expressions for $Q_A$, Note that this is a cubic equation in $Q_A$ and thus will always have a real root. But, we need $Q_A$ to be in the range $[0,1]$. The the values of $Q_A$ satisfying the above equality for a fixed value of $p$ are :

\(\begin{align} r_1 & = \frac{4 \sqrt[3]{3} p^9+\sqrt[3]{2} \left(\sqrt{81 p^{24}-96 p^{27}}-9 p^{12}\right)^{2/3}}{6^{2/3} p^6 \sqrt[3]{\sqrt{81 p^{24}-96 p^{27}}-9 p^{12}}}\\ r_2 & = -\frac{4 \sqrt[3]{3} p^9+\sqrt[3]{2} \left(\sqrt{81 p^{24}-96 p^{27}}-9 p^{12}\right)^{2/3}}{2\ 6^{2/3} p^6 \sqrt[3]{\sqrt{81 p^{24}-96 p^{27}}-9 p^{12}}} + i \left(\frac{ \left(3^{5/6} \left(2 \sqrt{81 p^{24}-96 p^{27}}-18 p^{12}\right)^{2/3}-12 \sqrt[3]{2} \sqrt[6]{3} p^9\right)}{12 p^6 \sqrt[3]{\sqrt{81 p^{24}-96 p^{27}}-9 p^{12}}}\right)\\ r_3 & = \overline{r_2} \end{align}\)

The keen eye may notice that these are gross looking equations. As mentioned before, since our equation was cubic in $Q_A$, one of these is guaranteed to be real. The other two are either both real or both complex. What do we see when we plot these out as a function of $p$?

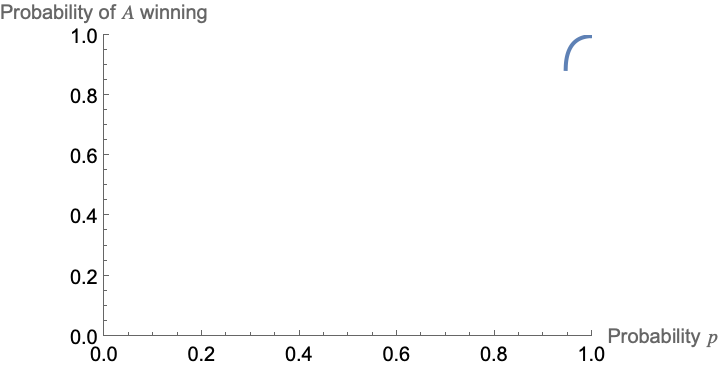
We see that for $p \leq\frac{3}{2^{5/3}} \approx 0.94 $, there is only one real root and it is negative. However, for $\boxed{p > \frac{3}{2^{5/3}}}$, the roots are all real with two positive and one negative. This value of $p$ comes from setting $p$ to ensure that the term $\sqrt{81 p^{24}-96 p^{27}}$ (which appears in each of the expressions for the roots), is real. Does this produce a valid probability value for $Q_A$? For $p$ just above this threshold value of $\hat{p} = \frac{3}{2^{5/3}}$, we see $Q_A$ has near repeated roots of around $\approx 0.88$, validating our solution. Interestingly the probability of winning is zero until $p > \hat{p}$ at which it jumps up to around $0.88$, as seen in the plot above!