This week’s The Fiddler on the Proof puzzle is paraphrased as follows:

You are planning a picnic on the remote tropical island of \(\pi\)-land. The island’s shape is a perfect semi-disk with two beaches, as illustrated below. We have Semicircular Beach (along the northern semicircular edge of the disk) and Diametric Beach (along the southern diameter of the disk).

Part 1:
If you pick a random spot on \(\pi\)-land for your picnic, what is the probability that it will be closer to Diametric Beach than to Semicircular Beach?

Part 2:
Given the radius of \(\pi\)-land is 1, on average, what will be the expected shortest distance to shore?

Illustration of the island
Figure 1: The island.

Solution

Part 1

The immediate intuition is that the set of points closer to the Diametric Beach than the Semicircular Beach should form a well-defined geometric region. If we can determine that region, denoted \(D\), the desired probability is simply the area of that region divided by the area of the entire semicircle.

Let the island’s radius be 1, its center be at \((0, 0)\), and denote the points on the island by the region \(C\). Consider a point \((x, y)\) on the island, which beach is it closer to? The distance to Diametric Beach is just its \(y\)-coordinate. What about the distance to Semicircular Beach?

The shortest path from \((x, y)\) to Semicircular Beach is along the radial line through \((0,0)\) and \((x,y)\).1 This means the shortest distance to the Semicircular Beach is given by:

\[1 - \sqrt{x^2 + y^2}\]

Therefore, for a point to be closer to the Diametric Beach than the Semicircular Beach, the following inequality must hold:

\[y \leq 1 - \sqrt{x^2 + y^2}\]

Rearranging:

\[y \leq \frac{1 - x^2}{2}\]

Thus, the region \(D\) of points closer to the Diametric Beach than the Semicircular Beach is:

\[D = \left\{ (x, y) \in C \mid y \leq \frac{1 - x^2}{2} \right\}.\]

This region is depicted below:

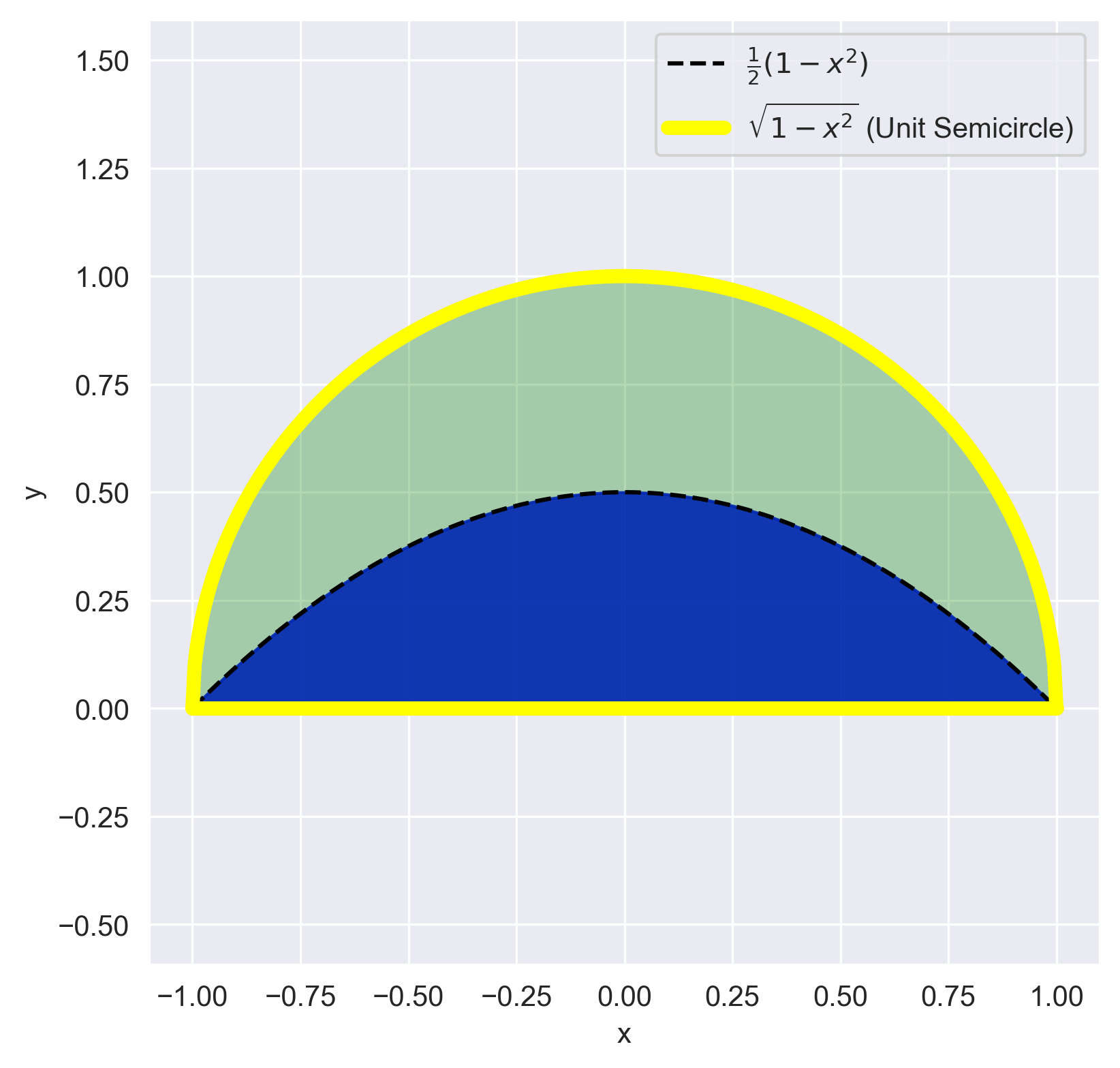
Geometric region solution
Figure 2: The region closer to the Diameter Beach than the Semicircular Beach (Blue).

Now, we compute the area of this region using integration:

\[\text{Area}(D) = \int_{-1}^1 \int_0^{\frac{1-x^2}{2}} dy \; dx = \frac{2}{3}.\]

Since the total area of the semicircle is \(\frac{\pi}{2}\), the probability of being closer to the Diametric Beach is:

\[\boxed{\frac{\text{Area}(D)}{\text{Area}(C)} = \frac{2/3}{\pi / 2} = \frac{4}{3\pi}}\]

Part 2

We’ve already done most of the heavy lifting in part 1)! Define \(L\) as the random variable representing the shortest distance to a beach. At a given point \((x, y) \in C\):

  • If \((x, y) \in D\), the shortest distance is \(y\).
  • If \((x, y) \in D^c\), the shortest distance is \(1 - \sqrt{x^2 + y^2}\).

Breaking up the expectation integral into two parts and solving yields:

\[\begin{align*} \mathbb{E}[L] & = \frac{1}{\pi /2} \int_C \min\left(y, 1 - \sqrt{x^2 + y^2}\right) dy \; dx \\ & = \frac{1}{\pi/2} \int_D y \; dy \; dx + \frac{1}{\pi/2} \int_{D^c} \left(1 - \sqrt{x^2 + y^2}\right) dy \; dx\\ & = \frac{1}{\pi/2} \int_{-1}^1\int_0^{\frac{1-x^2}{2}} y \; dy \; dx + \frac{1}{\pi/2} \int_{-1}^1\int_{\frac{1-x^2}{2}}^{\sqrt{1 - x^2}}1 - \sqrt{x^2 + y^2} \; dy \; dx\\ & = \boxed{\frac{1}{3} - \frac{4}{9 \pi}} \end{align*}\]

  1. Can you prove this? Hint: Use the triangle inequality. ↩