How Many Rabbits Can You Pull out of a Hat?

I found a new source of puzzles: the excellent Substack page The Fiddler on the Proof run by Zach Wissner-Gross. This week’s puzzle is paraphrased as follows:

Suppose I have a hat with \(3n\) small toy rabbits: \(n\) are red, \(n\) are green, and \(n\) are blue. I shuffle the rabbits around and randomly draw them out one at a time without replacement (i.e., once I draw a rabbit out, I never put it back in again).

Your job is to guess the color of each rabbit I draw. For each guess, you know the history of the rabbits already drawn. So if we’re down to the final rabbit in the hat, you should be able to predict its color with certainty.

Every time you correctly predict the color of the rabbit I draw, you earn a point. If you play optimally (i.e., to maximize your expected points), how many points can you expect to earn on average?

Solution

We can solve this using Dynamic Programming! We represent the current state as a tuple \((r, g, b)\), where \(r, g,\) and \(b\) denote the number of rabbits of each color remaining in the hat. Let \(J(r, g, b)\) be the maximum expected score starting from state \((r, g, b)\). Our goal is to determine \(J(n, n, n)\). We can solve for \(J(n, n, n)\) by developing a recurrence relation on the current state. We begin with the base cases.

Base Cases

• If there are no rabbits left, i.e., we are at state \((0, 0, 0)\), then there are zero points left to obtain, implying \(J(0, 0, 0) = 0.\)
• If any of \(r, g,\) or \(b\) are negative, we define: \(J\left(r, g, b \right) = 0, \; \text{if any } r < 0, g < 0, \text{or } b < 0.\) While negative rabbit counts don’t have any physical interpretation, this condition will allow us to greatly simplify our recurrence relation.

Recurrence Relation

For a general state where \(r, g, b \geq 0\) and at least one of them is positive, we can determine the expected points-maximizing guess for the next rabbit’s color by considering each option and selecting the best one. The probabilities for the next color of rabbit drawn are:

• The probability of drawing a red rabbit \(P_r = \frac{r}{r + g + b}\).
• The probability of drawing a green rabbit \(P_g = \frac{g}{r + g + b}\).
• The probability of drawing a blue rabbit \(P_b = \frac{b}{r + g + b}\).

Given these, the expected scores from guessing each color are:

\(J\left(r, g, b \mid \text{guess red}\right) = P_r \cdot (1 + J(r - 1, g, b)) + P_g\cdot J(r, g - 1, b) + P_b\cdot J(r, g, b - 1),\) \(J\left(r, g, b \mid \text{guess green}\right) = P_r\cdot J(r - 1, g, b) + P_g\cdot (1 + J(r, g - 1, b)) + P_b\cdot J(r, g, b - 1),\) \(J \left(r, g, b \mid \text{guess blue}\right) = P_r\cdot J(r - 1, g, b) + P_g\cdot J(r, g - 1, b) + P_b\cdot (1 + J(r, g, b - 1)).\)

To find the optimal expected score at state \((r, g, b)\), we take the maximum over these three choices.

The optimal guess is the color that achieves this maximum.

Implementation

Now that we have a recursive formulation, we can efficiently compute \(J(r, g, b)\) using dynamic programming. Let’s code this up in Python¹!

from functools import cache

@cache
def max_points(r, g, b):
""" Returns the maximum expected score under optimal play from the state
(r, g, b) """
    # Base Cases
    if r < 0 or g < 0 or b < 0:
        return 0
    elif r == 0 and g == 0 and b == 0:
        return 0
    # Main recurrence Case 
    if r > 0 or g > 0 or b > 0:
        total_rabbits = r + g + b
        Pr, Pb, Pg = r / total_rabbits, b / total_rabbits, g / total_rabbits
        
        guess_red = (Pr * (1 + max_points(r - 1, g, b)) +  
            Pg * max_points(r, g - 1, b) +
            Pb * max_points(r, g, b - 1))
        
        guess_green = (Pg * (1 + max_points(r, g-1, b)) +
            Pr * max_points(r - 1, g, b) +
            Pb * max_points(r, g, b - 1))
                       
        guess_blue = (Pb * (1 + max_points(r, g, b - 1)) +
            Pr * max_points(r - 1, g, b) +
            Pg * max_points(r, g - 1, b))
        
        return max(guess_green, guess_red, guess_blue)

def optimal_score(n):
  """ The value of J(n, n n) and the answer to our puzzle. """
    return max_points(n, n, n)

Now, if we plot the value of \(J(n, n, n)\) as a function of \(n\), we obtain Figure 1. Here we see that under the optimal guessing strategy, the expected score seems to grow roughly like \(\sim \frac{n}{3}\). In fact, we can actually note that \(\frac{n}{3}\) is a lower bound on the optimal expected score because it can be obtained with certainty by choosing one color of rabbit and guessing that color each turn until the game ends. We call this naive strategy the “stubborn guessing” strategy (since you refuse to change your guess each turn).

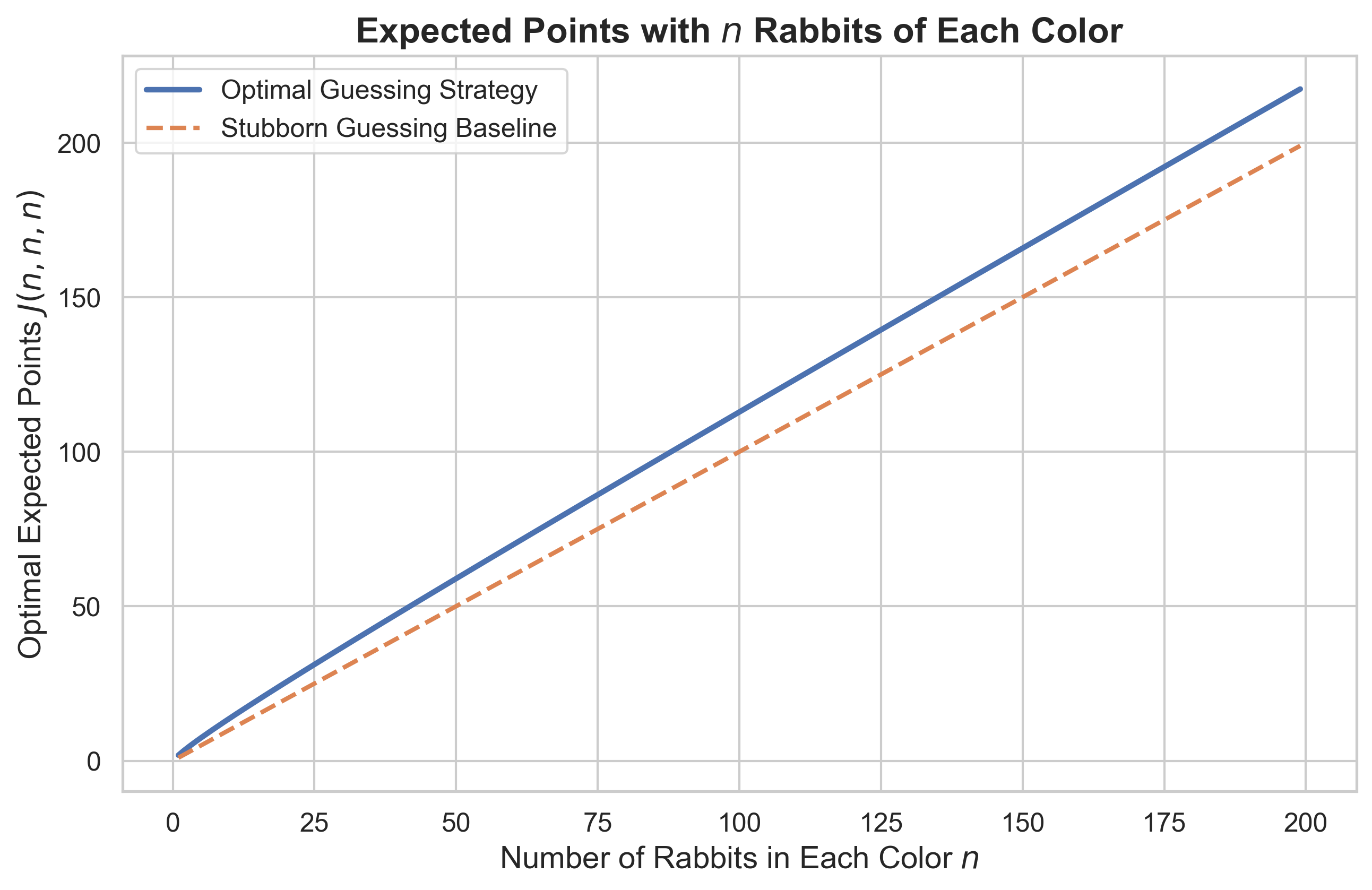
We can see that our optimal strategy does outperform the stubborn guessing strategy, but not by too much!

Okay, we have found a way to compute the expected number of points we can score under the optimal guessing strategy, but what actually is the optimal guessing strategy?. By recording the optimal guess at each step in our recursion, we can observe the optimal strategy has a simple form:

At any given state, guess a color that has the most rabbits remaining in the hat.

This makes sense intuitively, and this simple rule provides us with the best heuristic for maximizing our expected score.