Can You Root for the Underdog?

This week’s The Fiddler on the Proof puzzle is paraphrased as follows:

There are \(2^n\) teams playing in a single-elimination seeded tournament. The teams play in a traditional seeded tournament format. That is, in the first round, the sum of teams playing each other is \(2^n + 1\) (for example seed \(1\) plays seed \(2^n\), \(2\) plays \(2^n - 1\), etc). If the stronger team always advances, then the sum of opponents’ seeds in the second round is \(2^{n - 1} + 1\), and so on.

Each team possesses a “power index” equal to \(2^n + 1\) minus that team’s seed. For example, team \(1\) has power index \(2^n\). In any given matchup, the team with the greater power index would emerge victorious. However, March Madness fans love to root for the underdog. As a result, the team with the lower power index gets an effective “boost” \(B\) applied to their power index, where \(B\) is some positive non-integer.

As an illustration, consider the matchup between the \(2\) and \(3\)-seeds. The favored \(2\)-seed has a power index of \(3\), while the underdog \(3\)-seed has a power index of \(2+B\). When \(B\) is greater than \(1\), the \(3\)-seed will defeat the \(2\)-seed in an upset.

Depending on the value of \(B\), different teams will win the tournament. Of the \(2^n\) teams, how many can never win, regardless of the value of \(B\)?

Solution

We can start out with some observations. First, for fixed \(B\), the winner of the tournament is deterministic. This suggests we should define a function \(W_n(B)\) that for a given \(n\) and \(B\) returns the winning seed in the tournament. To solve our problem, we could then determine which values that \(W_n(B)\) can and cannot take on. The next useful observation is that for \(B > 2^n - 1\), the value of \(W_n(B)\) is a constant. Specifically, for \(B > 2^n - 1\), the lowest seeded team will always win the tournament. Thus we need only consider the non-integral values of \(W_n(B)\) on the interval \(B \in [0, 2^n]\). The last observation we need to consider is that for any two teams playing, say with seeds \(a\) and \(b\) with \(a < b\), the value of \(B\) for which the winner and loser of the game swap is \(b - a + \epsilon\) where \(\varepsilon > 0\) is an arbitrarily small constant. Therefore, as we vary \(B\) from \(0 \to 2^n\), the only values of \(B\) where we may see the value of \(W_n(B)\) change are of the form \(k + \varepsilon\) where \(k\) is a non-negative integer.

With those observations, our strategy for solving the problem can be made clear. For \(B = k + \varepsilon\) for \(k \in [2^n - 1]\), determine the value of \(W_n(B)\) for the given value of \(B\) and keep track of the winners as we iterate over the values of \(B\). Then simply report the values in \([2^n]\) that were not found to be winners.

from collections import defaultdict
import numpy as np

def gen_bracket(n):
    """
    Recursively generate a seeded bracket for n players (n must be a power of 2).
    Returns a list where consecutive elements form a matchup.
    """
    if n == 1:
        return [1]
    else:
        prev = gen_bracket(n // 2)
        mirror = [n + 1 - seed for seed in prev]
        bracket = [seed for pair in zip(prev, mirror) for seed in pair]
        return bracket

def winner(seedA, seedB, N, B):
    """
    Returns the winner of the matchup seedA vs seedB in an 
    N person tournament with boost B.
    """
    # make sure seedA is lower seed 
    if seedA > seedB:
        seedA, seedB = seedB, seedA
    power_rankA = N + 1 - seedA
    power_rankB = N + 1 - seedB + B
    if power_rankA > power_rankB:
        return seedA
    else:
        return seedB
    

def W(n, B):
    """ 
    The winner of a 2^n person tournament with boost B. 
    """
    N = 2 ** n 
    bracket = generate_bracket(N)
    while True:
        # keep simulating until one team left 
        if len(bracket) == 1:
            return bracket[0]
        else:
            winners = []
            for i in range(0, len(bracket), 2):
                seedA = bracket[i]
                seedB = bracket[i + 1]
                winners.append(winner(seedA, seedB, N, B))
            bracket = winners

Then to get the possible winners for a given tournament size of \(2^n\) and to compute the number of teams that cannot win, we can run the below code.

n = 6 # solve for 2^6 = 64 teams 
    
can_win = defaultdict(bool)
# B-values where winner could swap values
B_space = [i + eps for i in range(1, 2 ** n + 1)] 
for b in B_space:
    champ = tournament_winner(n, b)
    can_win[champ] = True
winners = list(sorted(list(can_win.keys())))
print(f'The teams that CAN win are {winners}')
print(f'There are {2 ** n  - len(winners)} teams that cannot win')
print(f'The function that predicts this is {2 ** (n - 1) - (n - 1)}')

Since this code is for general \(n\), we can compute the number of teams that cannot win for several values of \(n\), see table 1.

Some of you may notice a pattern in this sequence. If we let \(a_n\) be the number of teams that cannot win in a \(2^n\) team tournament, then we see the pattern emerge

for \(n \geq 2\). Which would suggest that

We won’t attempt prove this conjecture here, but the pattern holds for \(n \leq 20\).

Lastly, it would be interesting to see the plot of \(W_n(B)\) for various \(n\) so that we can get a sense of which teams are capable of winning. Below in Figure 1 is a gif that illustrates the function \(W_n(B)\) for various values of \(n\). We see that as \(n\) grows the shape of the function begins to approach some interesting limiting shape!

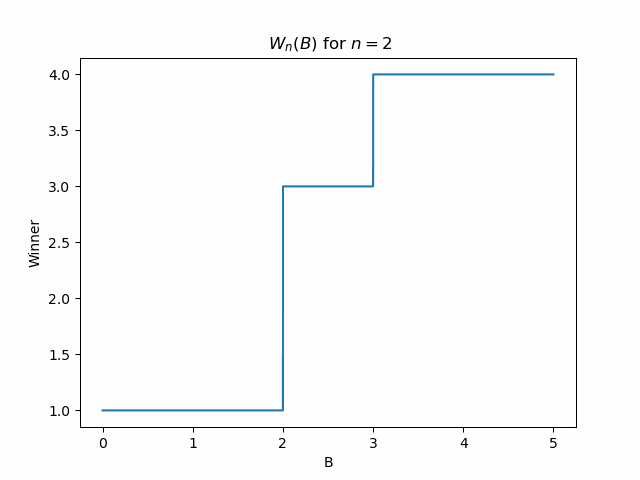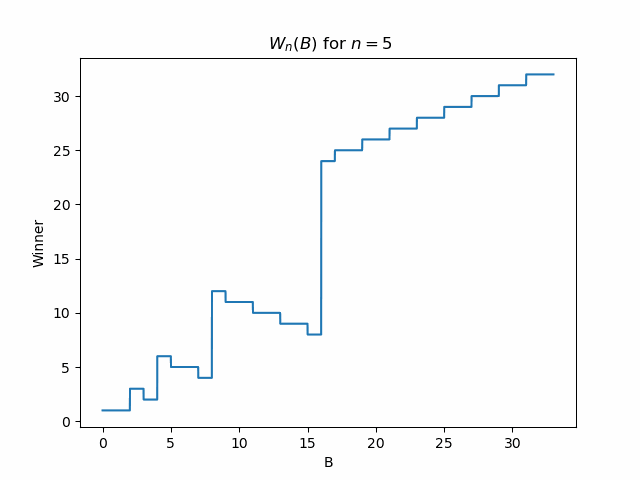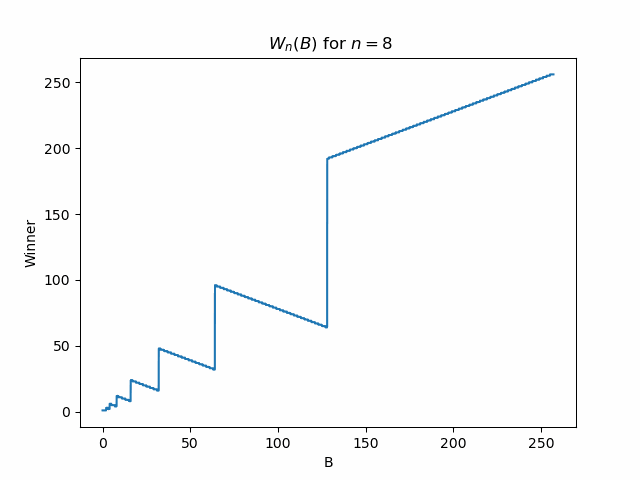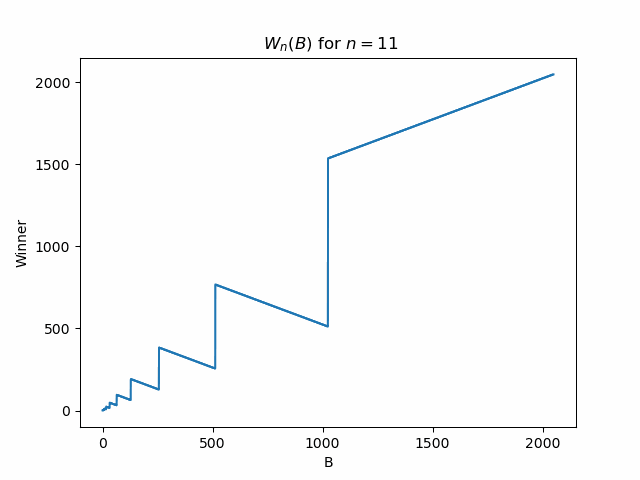
Upon inspection it appears there is a recursive description of how these curves relate to one another. Here is a very rough description of how they appear related. We see for a given \(n\), for \(B > 2^{n - 1}\), the \(W_n(B)\) is non-decreasing in \(B\) and produces \(2^{n - 2} + 1\) unique winners in that range. The curve for \(W_{n + 1}(B)\) has the same values as \(W_n(B)\) for \(B < 2^{n - 1}\). Then for \(B \in [2^{n - 1}, 2^n]\), the previously increasing portion of the curve is reflected downward about its start point, and then for \(B > 2^n\), the curve has the same monotonic behavior but for \(2^{n -1} + 1\) values. Note that for all \(n \geq 2\), \(W_n(B)\) is a one-to-one function. That is, no winner is ever repeated for different \(B\). If this behavior is indeed an accurate description of the curves (as it empirically appears to be), then this would prove our conjecture about \(a_n\) ¹.